已知菱形$\mathrm{ABCD}$，$\mathrm{P}, \mathrm{Q}, \mathrm{R}$和$\mathrm{S}$分别是边$\mathrm{AB}, \mathrm{BC}, \mathrm{CD}$和DA的中点。证明四边形$\mathrm{PQRS}$是矩形。

已知

$\mathrm{ABCD}$是菱形，$\mathrm{P}, \mathrm{Q}, \mathrm{R}$和$\mathrm{S}$分别是边$\mathrm{AB}, \mathrm{BC}, \mathrm{CD}$和DA的中点。

需要证明：我们需要证明四边形$\mathrm{PQRS}$是矩形。
 解答

连接$PQ,QR,RS,PS,AC$和$BD$。

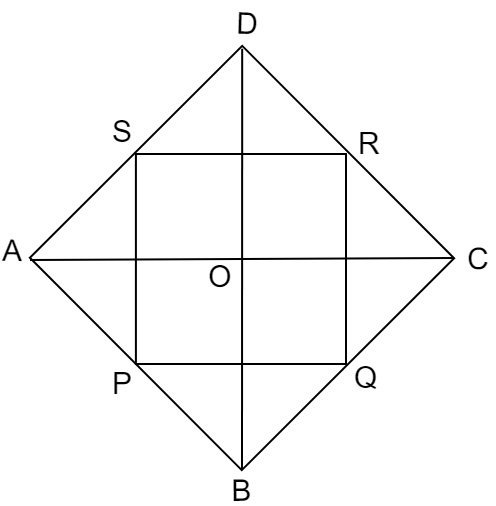
在$\triangle DRS$和$\triangle BPQ$中，

$DS = BQ$                 ($\frac{AD}{2}=\frac{BC}{2}$)

$\angle SDR = \angle QBP$         (菱形的对角相等)

$DR = BP$                   ($\frac{CD}{2}=\frac{AB}{2}$)

因此，根据SAS全等定理，我们得到，

$\triangle DRS \cong \triangle BPQ$

这意味着，

$RS = PQ$           (全等三角形对应边相等)............(i)

$在\triangle CQR$和$\triangle ASP$中，

$RC = PA$           ($\frac{CD}{2}=\frac{AB}{2}$)

$\angle RCQ = \angle PAS$             (菱形的对角)

$CQ = AS$           ($\frac{BC}{2}=\frac{AD}{2}$)

因此，根据SAS全等定理，我们得到，

$\triangle QCR \cong \triangle SAP$

这意味着，

$RQ = SP$         (全等三角形对应边相等)...............(ii)

在$\triangle CBD$中，

$R$和$Q$分别是$CD$和$BC$的中点。

这意味着，

$QR \| BD$

在$\triangle ABD$中，

$P$和$S$分别是$AD$和$AB$的中点。

这意味着，

$PS \| BD$

因此，

$QR \| PS$............(iii)

由(i)，(ii)和(iii)，我们得到，

$PQRS$是平行四边形。

$AB$是一条直线。

$\angle APS + \angle SPQ + \angle QPB = 180^o$

$BC$是一条直线。

$\angle PQB + \angle PQR + \angle CQR = 180^o$

$\angle APS + \angle SPQ + \angle QPB = \angle PQB + \angle PQR + \angle CQR$

$\angle APS + \angle SPQ + \angle QPB = \angle QPB + \angle PQR + \angle APS$

$\angle SPQ = \angle PQR$

$\angle SPQ + \angle PQR = 180^o$        (平行四边形的邻角互补)

$2\angle PQR = 180^o$

$PQR = 90^o$

在$PQRS$中，

$RS = PQ$

$RQ = SP$

$\angle Q = 90^o$

因此，

$PQRS$是矩形。

教程点

更新于: 2022年10月10日

62 次浏览

开启你的职业生涯

完成课程获得认证

开始学习