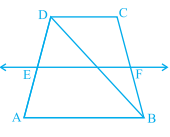
已知梯形\( \mathrm{ABCD} \)中，\( \mathrm{AB} \| \mathrm{DC} \)，\( \mathrm{BD} \)为对角线，\( \mathrm{E} \)为\( \mathrm{AD} \)的中点。过E作一条平行于\( \mathrm{AB} \)的直线，交\( \mathrm{BC} \)于\( \mathrm{F} \)（见下图）。求证：\( \mathrm{F} \)是\( \mathrm{BC} \)的中点。

已知

梯形\( \mathrm{ABCD} \)中，\( \mathrm{AB} \| \mathrm{DC} \)，\( \mathrm{BD} \)为对角线，\( \mathrm{E} \)为\( \mathrm{AD} \)的中点。

过E作一条平行于\( \mathrm{AB} \)的直线，交\( \mathrm{BC} \)于\( \mathrm{F} \)

证明：
我们需要证明\( \mathrm{F} \)是\( \mathrm{BC} \)的中点。

 解答

设\(BD\)与\(EF\)的交点为$P$。

在$\triangle ABD$中，

$EP \| AB$

$E$是$AD$的中点。

我们知道：

三角形一条边上的中点与另一边平行的直线，必平分第三边。

因此：

$P$是$BD$的中点。

在$\triangle BCD$中，

$PF \| CD$

$P$是$BD$的中点。

根据中点定理的逆定理：

$F$是$CB$的中点。

证毕。

更新于：2022年10月10日

41 次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告