数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学已知梯形ABCD中，AB平行于DC。一条平行于AC的直线与AB相交于X，与BC相交于Y。求证：三角形ADX的面积等于三角形ACY的面积。
[提示：连接CX。]
已知
梯形ABCD中，AB平行于DC。一条平行于AC的直线与AB相交于X，与BC相交于Y。
求证
我们必须证明三角形ADX的面积等于三角形ACY的面积。
解答
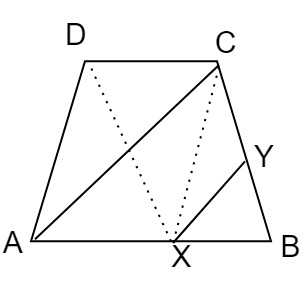
AC平行于XY
连接CX, AY和DX
三角形ADX和三角形ACX同底AX，且在平行线AB和DC之间。
因此，
三角形ADX的面积 = 三角形ACX的面积……(i)
三角形ACX和三角形ACY同底AC，且在平行线AC和XY之间。
因此，
三角形ACX的面积 = 三角形ACY的面积……(ii)
由(i)和(ii)可得，
三角形ADX的面积 = 三角形ACX的面积 = 三角形ACY的面积
这意味着，
三角形ADX的面积 = 三角形ACY的面积
证毕。
更新于：2022年10月10日
45 次浏览
广告