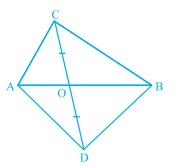
在下图中，△ABC和△ABD是同底AB的两个三角形。如果线段CD被AB平分于O，证明ar(△ABC) = ar(△ABD)。

已知

△ABC和△ABD是同底AB的两个三角形。

线段CD被AB平分于O。

要求

我们必须证明ar(△ABC) = ar(△ABD)。

解答

CO = OD

作CL⊥AB，DM⊥AB

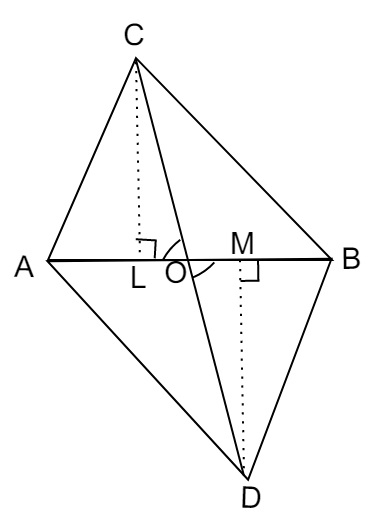
在△CLO和△DMO中，

∠L=∠M

CO=OD

∠COL=∠DOM (对顶角)

因此，根据AAS公理，

△CLO ≅ △DMO

这意味着，

CL=DM (全等三角形的对应边相等)

ar(△ABC) = 1/2 × 底 × 高

= 1/2 × AB × CL .........(i)

ar(△ADB) = 1/2 × AB × DM

= 1/2 × AB × CL .........(ii) (因为DM=CL)

(证明完毕)
由(i)和(ii)，我们得到：

ar(△ABC) = ar(△ABD)

证毕。

Tutorialspoint

更新于：2022年10月10日

浏览量：35

开启你的职业生涯

完成课程获得认证

开始学习