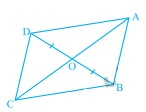
在下图中，四边形ABCD的对角线AC和BD相交于O。
如果AB=CD，则证明
(i) ar(DOC)=ar(AOB)
(ii) ar(DCB)=ar(ACB)
(iii) DA∥CB或ABCD是平行四边形。
[提示：从D和B分别向AC作垂线。]
"\n

---

已知

在四边形ABCD中，对角线AC和BD相交于O，使得OB=OD。

AB = CD。

要求

我们必须证明

(i) ar(DOC)=ar(AOB)
(ii) ar(DCB)=ar(ACB)
(iii) DA∥CB或ABCD是平行四边形。

解答

作DP⊥AC和BQ⊥AC。

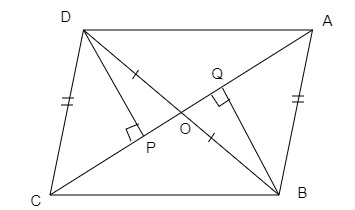
(i) 在△DOP和△BOQ中，

∠DPO = ∠BQO=90°

∠DOP = ∠BOQ（对顶角）

OD = OB（已知）

因此，根据AAS全等

△DOP ≅ △BOQ

这意味着，

DP = BQ----(i)（CPCT）

ar(DOP) = ar(BOQ)----(ii)（因为全等三角形的面积相等）

在△CDP和△ABQ中，

∠CPD = ∠AQB=90°

CD = AB（已知）

DP = BQ [来自公式(i)]

因此，根据RHS全等

△CDP ≅ △ABQ

这意味着，

ar(CDP) = ar(ABQ)...........(iii)（因为全等三角形的面积相等）

将公式(ii)和(iii)相加，我们得到，

ar(DOP) + ar(CDP) = ar(BOQ) + ar(ABQ)

ar (DOC) = ar (AOB)

(ii) ar (DOC) = ar (AOB)

这意味着，

ar (DOC) + ar (BOC) = ar (AOB) + ar (BOC) [两边加上ar (BOC)]

ar(DCB) = ar (ACB)

(iii) △DCB和△ACB的面积相等，且具有相同的底边。

这意味着，

△DCB和△ACB必须位于相同的平行线之间。

因此，

DA ∥ CB

ar(DOP) = ar(BOQ)

这意味着，

∠OBQ = ∠PDO…(iv)

ar(CDP) = ar(ABQ)

这意味着，

∠ABQ= ∠CDP….....(v)

将(iv)和(v)相加，我们得到，

∠OBQ+∠ABQ = ∠CDP + ∠PDO

∠ABO=∠CDO

∠CDB= ∠ABD

这意味着，

CD ∥ AB

因此，ABCD是平行四边形。