已知ABCD是一个矩形，P、Q、R、S分别是AB、BC、CD、DA的中点。证明四边形PQRS是菱形。

已知

ABCD是一个矩形，P、Q、R、S分别是AB、BC、CD、DA的中点。

要求：
我们必须证明四边形PQRS是菱形。
 解答

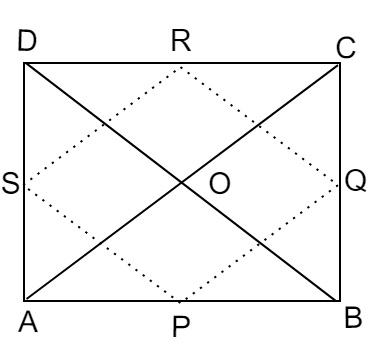
∠A=∠B=∠C=∠D=90°

AD=BC 且 AB=CD

P、Q、R、S分别是AB、BC、CD、DA的中点。

这意味着：

PQ ∥ AC

PQ = AC/2

RS ∥ AC

RS = AC/2

PQ = SR

在△ASP和△BQP中

AP = BP

AS = BQ

∠A = ∠B = 90°

因此，根据SAS全等，我们得到：

△ASP ≅ △BQP

这意味着：

SP = PQ (全等三角形对应边相等)

在△RDS和△RCQ中：

SD = CQ

DR = CR

∠C = ∠D = 90°

因此，根据SAS全等，我们得到：

△RDS ≅ △RCQ

这意味着：

SR = RQ (全等三角形对应边相等)

这里：

PQ = QR = RS = SP

因此，四边形PQRS是菱形。

教程点

更新于：2022年10月10日

浏览量：60

开启你的职业生涯

完成课程获得认证

开始学习