数据结构
网络
关系型数据库管理系统
操作系统
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
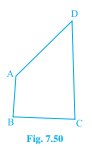
法律研究\( \mathrm{AB} \) and \( \mathrm{CD} \) are respectively the smallest and longest sides of a quadrilateral \( \mathrm{ABCD} \) (see Fig. 7.50). Show that \( \angle A>\angle C \) and \( \angle \mathrm{B}>\angle \mathrm{D} \).
"\n
已知
$AB$ 和 $CD$ 分别是四边形 $ABCD$ 的最短边和最长边。
要求
我们需要证明 $\angle A>\angle C$ 且 $\angle B>\angle $D$。
解答
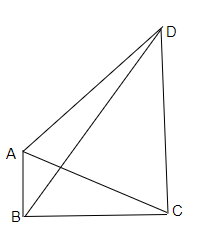
考虑 $\triangle ABD$，我们有：
$AB
我们知道：
对边较长的角总是较大。
这意味着：
$\angle ADB
类似地，在 $\triangle BCD$ 中：
我们有：
$BC
这意味着：
$\angle BDC
将 (i) 和 (ii) 相加，我们得到：
$\angle ADB +\angle BDC
这意味着：
$\angle ADC
$\angle B > \angle D$
类似地，在三角形 $ABC$ 中：
我们知道对边较长的角总是较大。
$\angle ACB
类似地，从 $\triangle ADC$ 中：
我们得到：
$\angle DCA
将 (iii) 和 (iv) 相加，我们得到：
$\angle ACB + \angle DCA
这意味着：
$\angle BCD
因此：
$\angle A > \angle C$。
更新于: 2022年10月10日
48 次查看
广告