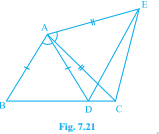
如图 7.21，\( \mathrm{AC}=\mathrm{AE}, \mathrm{AB}=\mathrm{AD} \) 且 \( \angle \mathrm{BAD}=\angle \mathrm{EAC} \)。证明 \( \mathrm{BC}=\mathrm{DE} \)。
"\n

已知

$AC=AE,AB=AD$ 且 $\angle BAD=\angle EAC$。

要求

我们需要证明 $BC=DE$。

解答

在 $\angle BAD=\angle EAC$ 的两边都加上 $\angle DAC$，得到：

$\angle BAD+\angle DAC=\angle EAC+\angle DAC$

这意味着：

$\angle BAC=\angle EAD$

我们知道：

根据边角边全等定理

如果两个三角形的一对对应边及其夹角分别相等，则这两个三角形全等。

已知：

$AC=AE$ 且 $AB=AD$

我们也有：

$\angle BAC=\angle EAD$

因此：

$\triangle ABC \cong \triangle ADE$。

我们还知道：

根据全等三角形对应边相等：如果两个三角形全等，则它们的所有对应边都必须相等。

因此：

$BC=DE$。

教程点

更新于: 2022年10月10日

29 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习