AD是等腰三角形ABC的高，其中AB=AC。
(i) 证明AD平分BC
(ii) 证明AD平分∠A。

已知

AD是等腰三角形ABC的高，其中AB=AC。

要求

我们必须证明：
(i) AD平分BC
(ii) AD平分∠A。

解答

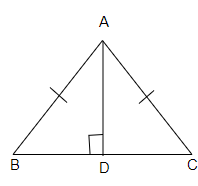
考虑三角形ABD和ACD。

已知AD是三角形ABD和ACD的高。

因此，∠ADB=∠ADC=90°。

我们有AB=AC。

由于AD是公共边，我们得到：

AD=DA

因此，

我们知道，根据RHS定理，如果一个直角三角形的斜边和一条直角边分别等于另一个直角三角形的斜边和一条直角边，那么这两个直角三角形全等。

因此，

三角形ABD ≅ 三角形ACD

我们也知道，

全等三角形的对应边相等。

因此，

BD=CD

因此，AD平分BC。

(ii) 同样，根据全等三角形的对应边相等：

我们也知道

全等三角形的对应角相等。

因此，

AD平分∠A。

教程点

更新于：2022年10月10日

浏览量：57

开启你的职业生涯

完成课程获得认证

开始学习