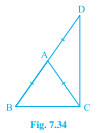
\( \triangle \mathrm{ABC} \) is an isosceles triangle in which \( \mathrm{AB}=\mathrm{AC} \). Side \( \mathrm{BA} \) is produced to \( \mathrm{D} \) such that \( \mathrm{AD}=\mathrm{AB} \) (see Fig. 7.34). Show that \( \angle \mathrm{BCD} \) is a right angle.
"\n

已知

$\triangle ABC$ 是一个等腰三角形，其中  $AB=AC$。边 $BA$ 延长到 $D$，使得 $AD=AB$。 

要求

我们需要证明 $\angle BCD$ 是直角。

解答
让我们考虑 $\triangle ABC$，

已知，

AB = AC 

我们知道，

等边对等角。

这意味着，

$\angle ACB = \angle ABC$ 

现在，让我们考虑 $\triangle ACD$

已知，

AD = AB

我们知道，

等边对等角。

这意味着，

$\angle ADC= \angle ACD$ 

我们知道，

三角形内角和始终等于 $180^o$

这意味着

在 $\triangle ABC$ 中，

$\angle CAB+\angle ACB+\angle ABC = 180^o$

因此，

$\angle CAB + 2\angle ACB=180^o$

这意味着，

$\angle CAB = 180^o–2\angle ACB$.........(i)

同样地，

在 $\triangle ADC$ 中，

$\angle CAD = 180^o – 2\angle ACD$......(ii)

此外，由于 $BD$ 是一条直线，

我们得到，

$\angle CAB + \angle CAD = 180^o$

将 (i) 和 (ii) 相加，我们得到，

$\angle CAB+\angle CAD=180^o–2\angle ACB+180^o–2\angle ACD$

$180^o=360^o–2\angle ACB-2\angle ACD$

$2(\angle ACB+\angle ACD)=180^o$

$\angle BCD=90^o$.

Tutorialspoint

更新于: 2022年10月10日

32 次浏览

开启您的 职业生涯

通过完成课程获得认证

开始学习