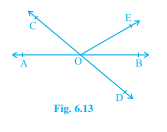
如图 6.13 所示，直线$\mathrm{AB}$和$\mathrm{CD}$相交于$\mathrm{O}$。如果$\angle \mathrm{AOC}+\angle \mathrm{BOE}=70^{\circ}$且$\angle \mathrm{BOD}=40^{\circ}$，求$\angle \mathrm{BOE}$和$\angle \mathrm{COE}$的反射角。
"\n

已知

直线 $AB$ 和 $CD$ 相交于 $O$。

$\angle AOC + \angle BOE = 70^o$ 且 $\angle BOD = 40^o$

要求

我们需要求出 $\angle BOE$ 和 $\angle COE$ 的反射角。

解答

$AOB$ 是一条直线。

因此，

$\angle AOC + \angle COE + \angle BOE = 180^o$

$(\angle AOC + \angle BOE) + \angle COE = 180^o$

$70^o + \angle COE = 180^o$

$\angle COE = 180^o-70^o= 110^o$

$\angle AOC = \angle BOD = 40^o$                (对顶角)

$\angle AOC + \angle BOE = 70^o$

这意味着，

$\angle BOD + \angle BOE = 70^o$

$\angle BOE = 70^o - 40^o = 30^o$

$\angle COE$ 的反射角 $= 360^o - \angle COE$

$= 360^o- 110^o$

$= 250^o$

因此，$\angle BOE = 30^o$ 且 $\angle COE$ 的反射角 $= 250^o$。

教程点

更新于: 2022年10月10日

39 次浏览

开启您的 职业生涯

完成课程获得认证

开始学习