在平行四边形$\mathrm{ABCD}$中，$\mathrm{E}$和$\mathrm{F}$分别是边$\mathrm{AB}$和$\mathrm{CD}$的中点（见下图）。证明线段AF和$\mathrm{EC}$三等分对角线BD。
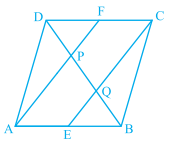"\n

已知

在平行四边形$\mathrm{ABCD}$中，$\mathrm{E}$和$\mathrm{F}$分别是边$\mathrm{AB}$和$\mathrm{CD}$的中点。

需要证明：
我们需要证明线段$AF$和$\mathrm{EC}$三等分对角线$BD$。

 解答

$A B C D$是一个平行四边形。

我们知道，

平行四边形的对边相等且平行。

这意味着，

$A B \| D C$

$A B=D C$

$\Rightarrow A E \| F C$

$\frac{1}{2} A B=\frac{1}{2} D C$

$\Rightarrow \mathrm{AE} \| \mathrm{FC}$

$\mathrm{AE}=\mathrm{FC}$

因此，

$AECF$是一个平行四边形。

这意味着，

$\mathrm{AF} \| \mathrm{EC}$

$\Rightarrow \mathrm{EQ} \| \mathrm{AP}$ 且 $\mathrm{FP} \| \mathrm{CQ}$

在$\triangle B A P$中，

$E$是$A B$的中点，且$E Q \| A P$。

根据中点定理的逆定理，

$Q$是$B P$的中点。

这意味着，

$\mathrm{BQ}=\mathrm{PQ}$...........(i)

在$\triangle D Q C$中，

$F$是$D C$的中点

$F P \| C Q$

根据中点定理的逆定理，

$P$是$D Q$的中点。

因此，

$\mathrm{PQ}=\mathrm{DP}$........(ii)

由(i)和(ii)可得，

$B Q=P Q=P D$

因此，$CE$和$AF$三等分对角线$BD$。

教程点

更新于： 2022年10月10日

35次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习