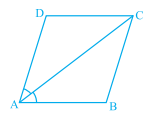
平行四边形ABCD的对角线AC平分∠A（见下图）。证明：
(i) 它也平分∠C；
(ii) ABCD是菱形。
"\n

已知：

平行四边形(ABCD)的对角线(AC)平分∠A。

要求

我们需要证明

(i) 它也平分∠C。

(ii) ABCD是菱形。

解答

(i) 这里，ABCD是一个平行四边形，对角线AC平分∠A。

∴ ∠DAC=∠BAC      ...... (1)

现在，

AB∥DC，AC为截线，

∴ ∠BAC=∠DCA          [ 内错角 ]  ...... (2)

AD∥BC，AC为截线，

∴ ∠DAC=∠BCA         [ 内错角 ]   .......(3)

由(1)、(2)和(3)

∠DAC=∠BAC=∠DCA=∠BCA

∴ ∠DCA=∠BCA

因此，AC平分∠C。

(ii) 在△ABC中，

⇒ ∠BAC=∠BCA      [ 上述已证]

⇒ BC=AB      [ 等角对等边]   ...... (1)

此外，AB=CD且AD=BC  [ 平行四边形的对边相等]  .. (2)

由(1)和(2)，

⇒ AB=BC=CD=DA

因此，ABCD是菱形。

教程点

更新于： 2022年10月10日

48 次浏览

开启你的职业生涯

通过完成课程获得认证

立即开始