已知$\mathrm{ABC}$ 是一个直角三角形，$\mathrm{C}$ 为直角顶点。过斜边$\mathrm{AB}$ 的中点$\mathrm{M}$ 且平行于$\mathrm{BC}$ 的直线交$\mathrm{AC}$ 于$\mathrm{D}$。证明：
(i) $\mathrm{D}$ 是$\mathrm{AC}$ 的中点
(ii) $\mathrm{MD} \perp \mathrm{AC}$
(iii) $\mathrm{CM}=\mathrm{MA}=\frac{1}{2} \mathrm{AB}$

已知

$\mathrm{ABC}$ 是一个直角三角形，$\mathrm{C}$ 为直角顶点。过斜边$\mathrm{AB}$ 的中点$\mathrm{M}$ 且平行于$\mathrm{BC}$ 的直线交$\mathrm{AC}$ 于$\mathrm{D}$。

求证：
我们需要证明：

(i) $\mathrm{D}$ 是$\mathrm{AC}$ 的中点
(ii) $\mathrm{MD} \perp \mathrm{AC}$
(iii) $\mathrm{CM}=\mathrm{MA}=\frac{1}{2} \mathrm{AB}$

 解答

$\mathrm{ABC}$ 是一个直角三角形，$\mathrm{C}$ 为直角顶点。

这意味着：

$\angle C=90^o$

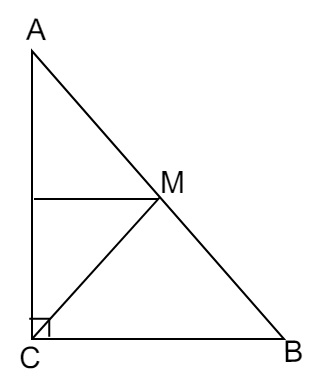
$M$ 是斜边 $AB$ 的中点。

$DM \| BC$

(i) 在 $\triangle \mathrm{ABC}$ 中，

$\mathrm{BC} \| \mathrm{MD}$ 

$\mathrm{M}$ 是 $\mathrm{AB}$ 的中点。

因此，根据中点定理的逆定理，我们得到：

$D$ 是 $AC$ 的中点。

(ii) $MD \| B C$ 且 $C D$ 是横截线。

这意味着：

$\angle A D M=\angle A C B=90^{\circ}$             (同位角相等)

$\Rightarrow \mathrm{MD} \perp \mathrm{AC}$

(iii) 在 $\triangle A D M$ 和 $\triangle C D M$ 中，

$\mathrm{DM}=\mathrm{DM}$          (公共边)

$AD=C D$        ($D$ 是 $AC$ 的中点)

$\angle \mathrm{ADM}=\angle \mathrm{MDC} = 90^{\circ}$

因此，根据 SAS 全等定理，我们得到：

$\triangle \mathrm{ADM}=\triangle \mathrm{CDM}$

这意味着：

$\mathrm{CM}=\mathrm{AM}$              (全等三角形对应边相等)......(i)

$M$ 是 $AB$ 的中点。

$\mathrm{AM}=\mathrm{BM}=\frac{1}{2} \mathrm{AB}$.......(ii)

由 (i) 和 (ii) 可得：

$\mathrm{CM}=\mathrm{AM}=\frac{1}{2} \mathrm{AB}$

证毕。

教程点

更新于： 2022年10月10日

60 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习