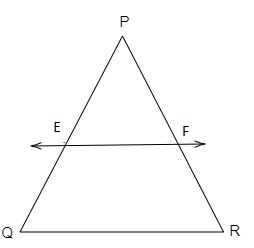
在$\triangle PQR$中，$E$和$F$分别是边$PQ$和$PR$上的点。对于以下每种情况，判断$EF \| QR$是否成立
(i) $PE = 3.9\ cm，EQ = 3\ cm，PF = 3.6\ cm$ 且 $FR = 2.4\ cm$
(ii) $PE = 4\ cm，QE = 4.5\ cm，PF = 8\ cm$ 且 $RF = 9\ cm$
(iii) $PQ = 1.28\ cm，PR = 2.56\ cm，PE = 0.18\ cm$ 且 $PF = 0.36\ cm$

待办事项

我们需要在每种情况下判断$EF \parallel QR$是否成立。

解答

(i) 我们知道：

如果一条直线将三角形的两边按比例分割，那么它平行于第三边。

$\frac{PE}{EQ}=\frac{3.9}{3}=1.3$

$\frac{PF}{FR}=\frac{3.6}{2.4}=\frac{3}{2}$

$\frac{PE}{EQ}≠\frac{PF}{FR}$

因此，根据比例线段定理的逆定理，$EF$不平行于$QR$。  

(ii) 我们知道：

如果一条直线将三角形的两边按比例分割，那么它平行于第三边。

$\frac{PE}{EQ}=\frac{4}{4.5}=\frac{8}{9}$

$\frac{PF}{FR}=\frac{8}{9}$

$\frac{PE}{EQ}=\frac{PF}{FR}$

因此，根据比例线段定理的逆定理，$EF$平行于$QR$。  

(iii) 我们知道：

如果一条直线将三角形的两边按比例分割，那么它平行于第三边。

$\frac{PQ}{PE}=\frac{1.28}{0.18}=\frac{64}{9}$

$\frac{PR}{PF}=\frac{2.56}{0.36}=\frac{64}{9}$

$\frac{PQ}{PE}=\frac{PR}{PF}$

因此，根据比例线段定理的逆定理，$EF$平行于$QR$。  

教程点

更新于：2022年10月10日

61 次查看

开启你的职业生涯

通过完成课程获得认证

开始学习