在△ABC和△PQR中，AB = PQ，BC = QR，CB和RQ分别延长到X和Y，且∠ABX = ∠PQY。证明△ABC ≅ △PQR。
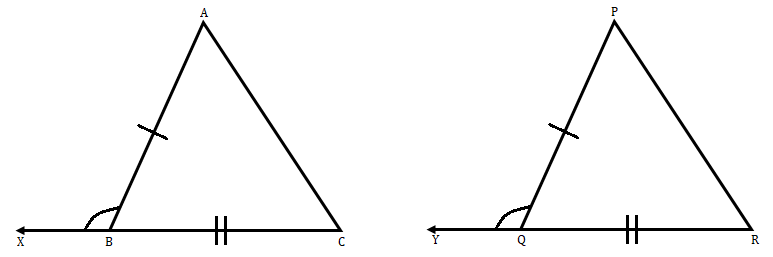"\n

已知：

AB = PQ，BC = QR

CB和RQ分别延长到X和Y

∠ABX = ∠PQY

证明：我们需要证明△ABC ≅ △PQR。

解答

∠ABC + ∠ABX = 180° (平角) ....(i)

∠PQR + ∠PQY = 180° (平角) ....(ii)

由(i)和(ii)

∠ABC + ∠ABX = ∠PQR + ∠PQY

已知，∠ABX = ∠PQY

∠ABC = ∠PQR ....(iii)

现在，在△ABC和△PQR中

AB = PQ (已知)

∠ABC = ∠PQR (由公式iii)

BC = QR (已知)

因此，根据SAS定理，△ABC ≅ △PQR。

Tutorialspoint

更新于：2022年10月10日

77 次浏览

开启你的职业生涯

完成课程获得认证

开始学习