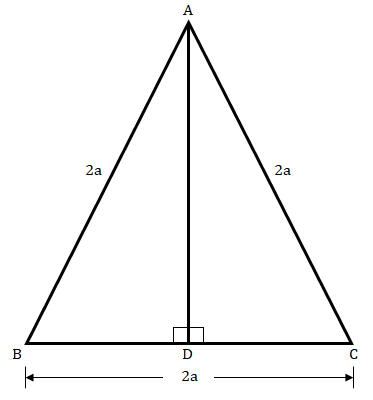
在$∆ABC$中，$AB\ =\ BC\ =\ CA\ =\ 2a$且$AD\ ⊥\ BC$。证明
(i) $AD\ =\ a\sqrt{3}$
(ii) 面积$(∆ABC)\ =\ \sqrt{3}a^2$
"\n

已知

在$∆ABC$中，$AB\ =\ BC\ =\ CA\ =\ 2a$且$AD\ ⊥\ BC$。

要求

我们需要证明

(i) $AD\ =\ a\sqrt{3}$ 

(ii) 面积$(∆ABC)\ =\ \sqrt{3}a^2$

解答

(i) 在$∆ABD$和$∆ACD$中，

$\angle ADB = \angle ADC = 90^o$

$AB = AC$  (已知)

$AD = AD$  (公共边)

因此，

$∆ABD ≅ ∆ACD$   (根据 RHS 全等定理)

这意味着，

$BD = CD = a$  (全等三角形的对应边相等)

在$∆ABD$中，

根据勾股定理，

$AD^2 + BD^2 = AB^2$

$AD^2 + a^2 = (2a)^2$

$AD^2 = 4a^2 – a^2 = 3a^2$

$AD = \sqrt{3a^2}$

$AD = \sqrt{3}a$

(ii) 面积$(∆ABC) = \frac{1}{2} \times BC \times AD$

                               $= \frac{1}{2} \times (2a) \times (\sqrt{3}a)$

                                $= \sqrt{3}a^2$

证毕。

教程点

更新于: 2022年10月10日

44 次查看

开启你的职业生涯

通过完成课程获得认证

开始学习