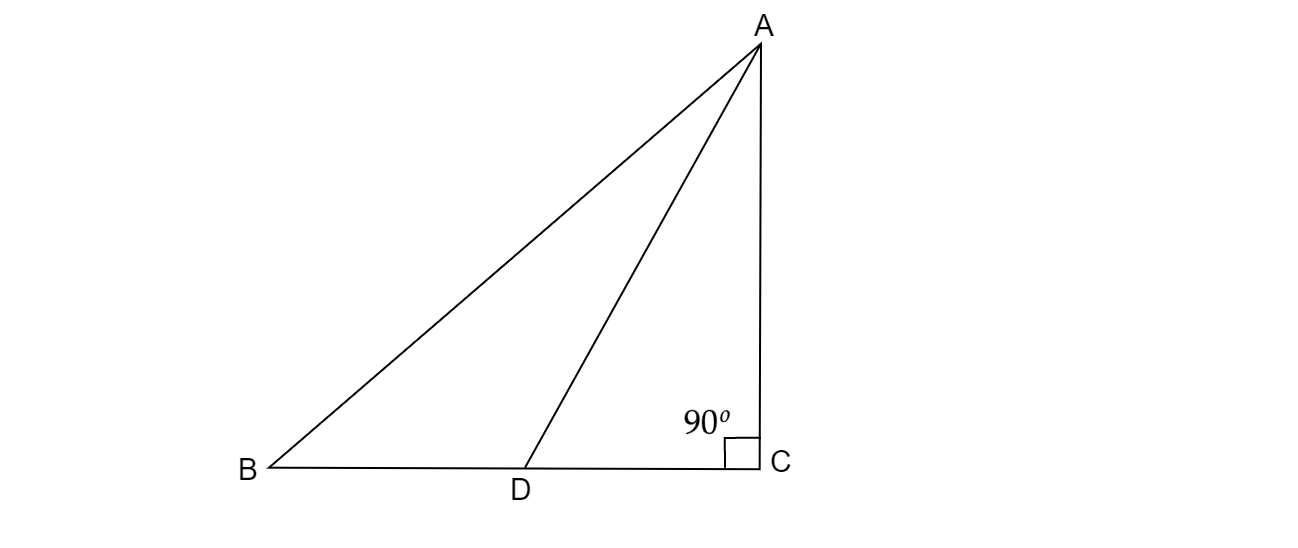
如图 3 所示，ABC 是一个直角三角形，∠C 为直角，D 是 BC 的中点，证明 $( AB)^{2} =4( AD)^{2} -3( AC)^{2} 。
"\n

已知：ABC 是一个直角三角形，∠C 为直角，D 是 BC 的中点。

求证：$( AB)^{2} =4( AD)^{2} -3( AC)^{2} 。

已知 $AC\bot BC$                 $( \because \vartriangle ABC\ 是\ 一个\ 直角\ 三角形)$

$BD=CD$                                       $(  \because \ D\ 是\ BC\ 的\ 中点)$

在 $\vartriangle$ABC 中，

$( 使用勾股定理)$

$( AB)^{2} =( BC)^{2} +( AC)^{2}$

 

$\Rightarrow ( AB)^{2} =( BD+CD)^{2} +( AC)^{2}$          $( \because \ BD+CD=BC)$ 

$\Rightarrow ( AB)^{2} =( CD+CD)^{2} +( AC)^{2}$

 

$\Rightarrow ( AB)^{2} =4( CD)^{2} +( AC)^{2}$                           $\dotsc \dotsc \dotsc \dotsc \dotsc \dotsc \dotsc ( 1)$ 

在三角形 $\vartriangle ADC$ 中

$( 使用勾股定理)$

$( AD)^{2} =( AC)^{2} +( CD)^{2}$                                     $( \because \vartriangle ADC\ 也\ 是\ 一个\ 直角\ 三角形)$ 

$\Rightarrow ( CD)^{2} =( AD)^{2} -( AC)^{2}$

将 $( CD)^{2}$ 的值代入方程 (1)

$\Rightarrow ( AB)^{2} =4\left(( AD)^{2} -( AC)^{2}\right) +( AC)^{2}$

$\Rightarrow ( AB)^{2} =4( AD)^{2} -4( AC)^{2} +( AC)^{2}$

$\Rightarrow ( AB)^{2} =4( AD)^{2} -3( AC)^{2}$

证毕。