在直角三角形ABC中，∠C=90°，如果D是BC的中点，证明AB²=4AD²-3AC²。

已知

在直角三角形ABC中，∠C=90°，D是BC的中点。

要求

我们必须证明AB²=4AD²-3AC²。

解答

D是BC的中点。因此，BC=2CD=2BD。

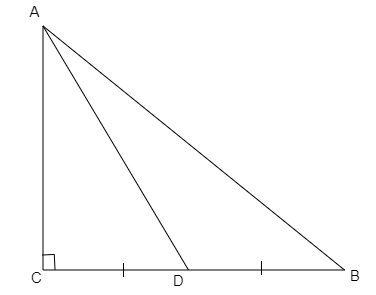
在△ABC中，根据勾股定理，

AB²=AC²+BC²

AB²=AC²+(2CD)² (BC=2CD)

AB²=AC²+4CD².....(i)

在△ACD中，根据勾股定理，

AD²=AC²+CD²

CD²=AD²-AC²....(ii)

将方程(ii)代入方程(i)，我们得到：

AB²=AC²+4(AD²-AC²)

AB²=AC²+4AD²-4AC²

AB²=4AD²-3AC²

证毕。

教程点

更新于：2022年10月10日

89 次浏览

开启你的职业生涯

完成课程获得认证

开始学习