数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
微软 Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会研究
服装研究
法律研究在下图中，D 是边 BC 的中点，且 AE ⊥ BC。如果 BC=a，AC=b，AB=c，ED=x，AD=p 且 AE=h，证明 b² + c² = 2p² + a²/2。
已知
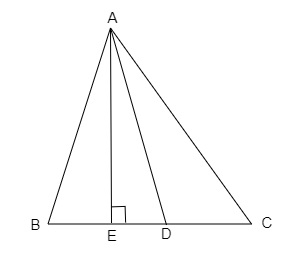
在给定图形中，D 是边 BC 的中点，且 AE ⊥ BC。
BC=a，AC=b，AB=c，ED=x，AD=p 且 AE=h。
要求
我们必须证明 b² + c² = 2p² + a²/2。
解答
在△AED 中，根据勾股定理，
AD² = AE² + ED²
AE² = AD² - ED².....(i)
在△AEC 中，根据勾股定理，
AC² = AE² + EC² b² = (AD² - ED²) + (ED + DC)² (由 (i) 得)
b² = AD² - ED² + ED² + DC² + 2ED × DC
b² = AD² + DC² + 2DC × ED
b² = p² + (a/2)² + 2 × (a/2) × x (因为 DC = BC/2)
b² = p² + a²/4 + ax......(ii)
在△AEB 中，根据勾股定理，
AB² = AE² + BE²
c² = (AD² - ED²) + (BD - ED)² (由 (i) 和 BE = BD - ED 得)
c² = AD² - ED² + BD² + ED² - 2BD × ED
c² = AD² + BD² - 2BD × ED
c² = p² + (a/2)² - 2 × (a/2) × x (因为 DC = BC/2)
c² = p² + a²/4 - ax......(iii)
将方程 (ii) 和 (iii) 相加，我们得到：
b² + c² = p² + a²/4 + ax + p² + a²/4 - ax
b² + c² = 2p² + 2 × a²/4
b² + c² = 2p² + a²/2
证毕。
更新于：2022年10月10日
60 次浏览
广告