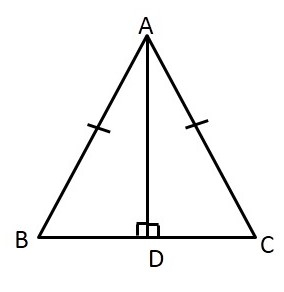
AD 是三角形对应边 BC 的高。证明 \( AB+AC+BC>2AD \)。

学术数学 NCERT 7 年级

已知：ABC 是一个三角形。

AD 是对应于 BC 的高。

要求:

我们必须证明 $AB+AC+BC>2AD$。

解答:

在三角形 ABD 中，

$AB+BD>AD$（三角形任意两边的和大于第三边）...(i)

在三角形 ACD 中，

$DC+AC>AD$.........(ii)

将方程 (i) 和 (ii) 相加，得到，

$AB+(BD+DC)+AC>AD+AD$

$AB+AC+BC>2AD$

证毕。

教程点

更新于： 2022-10-10

175 次浏览

相关文章
$\triangle ABC$ 是一个等腰三角形，使得 $AB=AC$，$AD \perp BC$ a) 证明 $\triangle ABD \cong \triangle ACD$ b) 证明 $\angle B=\angle C$ c) D 是 BC 的中点吗？"\n
在下图中，D 是边 BC 的中点，$AE \perp BC$。如果 \( BC=a, AC=b, AB=C, ED=x, AD=p \) 和 \( AE=h, \) 证明 \( b^{2}+c^{2}=2 p^{2}+\frac{a^{2}}{2} \)。"\n
在直角 \( \triangle ABC \) 中，∠C 为直角，如果 D 是 BC 的中点，证明 $BC^{2}=4(AD^{2}-AC^{2})$。
在下图中，D 是边 BC 的中点，$AE \perp BC$。如果 \( BC=a, AC=b, AB=C, ED=x, AD=p \) 和 \( AE=h, \) 证明 \( b^{2}=p^{2}+a x+\frac{a^{2}}{4} \)。"\n
在 \( \triangle ABC \) 中，$AD \perp BC$ 且 \( AD^{2}=BD . CD \)。证明 \( \angle BAC=90^o \)。"\n
在下图中，D 是边 BC 的中点，$AE \perp BC$。如果 \( BC=a, AC=b, AB=C, ED=x, AD=p \) 和 \( AE=h, \) 证明 \( c^{2}=p^{2}-a x+\frac{a^{2}}{4} \)。"\n
在直角三角形 \( ABC \) 中，其中 \( \angle C=90 \)，如果 D 是 BC 的中点，证明 \( AB^{2}=4 AD^{2}-3 AC^{2} \)。
在附图中，\( \Delta ABC \) 是一个等腰三角形，使得 \( AB=AC \)。边 BA 延长到 D，使得 $AD=AB$。证明 \( \angle BCD=90^{\circ} \)。 "\n
D 是 \( \triangle ABC \) 的边 BC 的中点。AD 在 E 点被平分，BE 的延长线与 AC 相交于点 \( X \)。证明 $BE:EX=3: 1$。
在四边形 \( ABCD \) 中，$\angle B=90^{\circ}$，$AD^{2}=AB^{2}+BC^{2}+CD^{2}$，证明 $\angle ACD=90^o$。
在 $\triangle ABC$ 中，边 $AB$ 延长到 $D$，使得 $BD = BC$。如果 $\angle B = 60^o$ 且 $\angle A = 70^o$，证明 $AD > CD$。
在 $\triangle ABC$ 中，边 $AB$ 延长到 $D$，使得 $BD = BC$。如果 $\angle B = 60^o$ 且 $\angle A = 70^o$，证明 $AD > AC$。
如果 \( A, B, C \) 是三角形 \( ABC \) 的内角，证明 \( \tan \left(\frac{C+A}{2}\right)=\cot \frac{B}{2} \)
如果 \( A, B, C \) 是三角形 \( ABC \) 的内角，证明 \( \sin \left(\frac{B+C}{2}\right)=\cos \frac{A}{2} \)
证明 $a^2 + b^2 + c^2 – ab – bc – ca$ 对所有 $a, b$ 和 $c$ 的值始终非负。

开启你的职业生涯

通过完成课程获得认证

广告

© . All rights reserved.