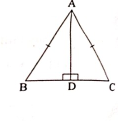
$\triangle ABC$ 是一个等腰三角形，其中 $AB=AC$，$AD \perp BC$
a) 证明 $\triangle ABD \cong \triangle ACD$
b) 证明 $\angle B=\angle C$ c) D 是 BC 的中点吗？
"\n

已知

$AB = AC$

$AD$ 垂直于 $BC$。

需要证明

a) 证明 $\triangle ABD \cong \triangle ACD$

b) 证明 $\angle B=\angle C$

c) D 是 BC 的中点吗？

解答

RHS 全等

在两个直角三角形中，如果一个三角形的斜边和一条边的长度等于另一个三角形的斜边和对应边的长度，则这两个三角形全等。

$AD$ 垂直于 $BC$。

$∠ADB = ∠ADC = 90°$

(a)

在 $△ABD$ 和 $△ACD$ 中，

$AB = AC$ (已知)

$AD = AD$ (公共边)

$∠ADB = ∠ADC = 90°$

因此，根据 RHS 全等，

$△ABD ≅ △ACD$

证毕。

(b)

$△ABD ≅ △ACD$，

这意味着，

$∠ABD = ∠ACD$ (全等三角形对应角相等)

证毕。

(c)

$△ABD ≅ △ACD$，

这意味着，

$BD = DC$ (全等三角形对应边相等)

因此，

D 是 BC 的中点。

Tutorialspoint

更新于: 2022年10月10日

77 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习