三角形$ABC$中，$\angle B = 2\angle C$，$D$是$BC$上一点，使得$AD$平分$\angle BAC$，且$AB = CD$。证明$\angle BAC = 72^o$。

已知

三角形$ABC$中，$\angle B = 2\angle C$，$D$是$BC$上一点，使得$AD$平分$\angle BAC$，且$AB = CD$。

要求

我们必须证明$\angle BAC = 72^o$。

解答

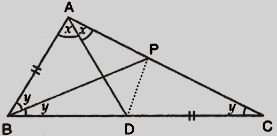
作$\angle A B C$的角平分线，交$AC$于$P$。

连接$PD$

设$\angle A C B=y$，$\angle B A D=\angle D A C=x$

$\angle B=\angle A B C=2 \angle C=2 y$

$\angle B A C=2 x$

因此，$AD$是$\angle BAC$的平分线

在$\triangle B P C$中

$\angle C B P=y$

因此，$BP$是$\angle A B C$的平分线

$\angle P C B=y$

$\angle C B P=\angle P C B=y$

这意味着，

$P C=B P$

在$\triangle \mathrm{ABP}$和$\triangle DCP$中，我们有，

$\angle \mathrm{ABP}=\angle \mathrm{DCP}=\mathrm{y}$

$\mathrm{AB}=\mathrm{DC}$

$\mathrm{PC}=\mathrm{BP}$

因此，根据SAS公理，

$\triangle \mathrm{ABP} \cong \triangle \mathrm{DCP}$

这意味着，

$\angle B A P=\angle C D P$

$A P=D P$            (对应边相等)

$\angle B A P=\angle C D P=2 x$

在$\triangle A B D$中，

$\angle \mathrm{ABD}+\angle B A D+\angle A D B=180^{\circ}$

$\angle A D B+\angle A D C=180^{\circ}$

$2 x+2 y+y=180^{\circ}$

$2 y+3 y=180^{\circ}$

$5 y=180^{\circ}$

$y=\frac{180^{\circ}}{5}$

$y=36^{\circ}$

因此，$x=y=36^{\circ}$

$\angle A=\angle B A C=2 x=2 \times 36^{\circ}=72^{\circ}$

因此，

$\angle B A C=72^{\circ}$

证毕。

教程点

更新于： 2022年10月10日

108 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习