D是三角形ABC的BC边上的一点，使得∠ADC = ∠BAC。证明CA² = CB·CD。

已知

D是三角形ABC的BC边上的一点，使得∠ADC = ∠BAC。

要求

我们必须证明CA² = CB·CD。

解答

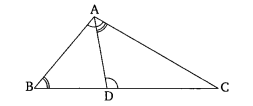
在△ABC和△DAC中，

∠C=∠C (公共角)

∠BAC=∠ADC

因此，根据AA相似准则，

△ABC ∽ △DAC

这意味着，

CA/CD = CB/CA

这意味着，

CA²=CB × CD

证毕。

Tutorialspoint

更新于：2022年10月10日

43 次浏览

开启你的职业生涯

完成课程获得认证

开始学习