已知圆的直径为 $AB$，弦 $AC$ 满足 $\angle BAC=30^{\circ}$，圆心为 $O$。过 $C$ 点的切线交 $AB$ 于点 $D$。求证：$BC=BD$。

已知

$AB$ 是圆的直径，$AC$ 是圆的弦，圆心为 $O$，且 $\angle BAC=30^{\circ}$。过 $C$ 点的切线交 $AB$ 于点 $D$。

要求

我们必须证明 $BC=BD$。

解答

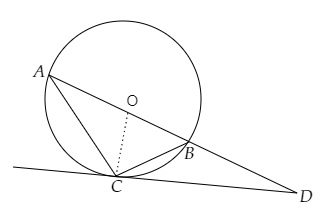
连接 $BC$ 和 $OC$。

$\angle BAC = 30^o$

$\Rightarrow \angle BCD = 30^o$    (切线与弦所成的角等于弦在圆周上所对的圆周角)

$\angle ACD = \angle ACO + \angle OCD$

$\angle ACD = 30^o + 90^o = 120^o$      ($OC\ \perp\ CD$ 且 $OA = OC$，$\angle OAC = \angle OCA = 30^o$)

在 $\triangle ACD$ 中，

$\angle CAD + \angle ACD + \angle ADC = 180^o$

$30^o + 120^o + \angle ADC = 180^o$

$\angle ADC = 180^o - (30^o + 120^o) = 30^o$

在 $\triangle BCD$ 中，

$\angle BCD = \angle BDC = 30^o$

$BC = BD$        (等角对等边)

证毕。

教程点

更新于: 2022年10月10日

72 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习