如图所示，$AB$是圆的弦，圆心为$O$，$AOC$是直径，$AT$是$A$点的切线。证明$∠BAT = ∠ACB$。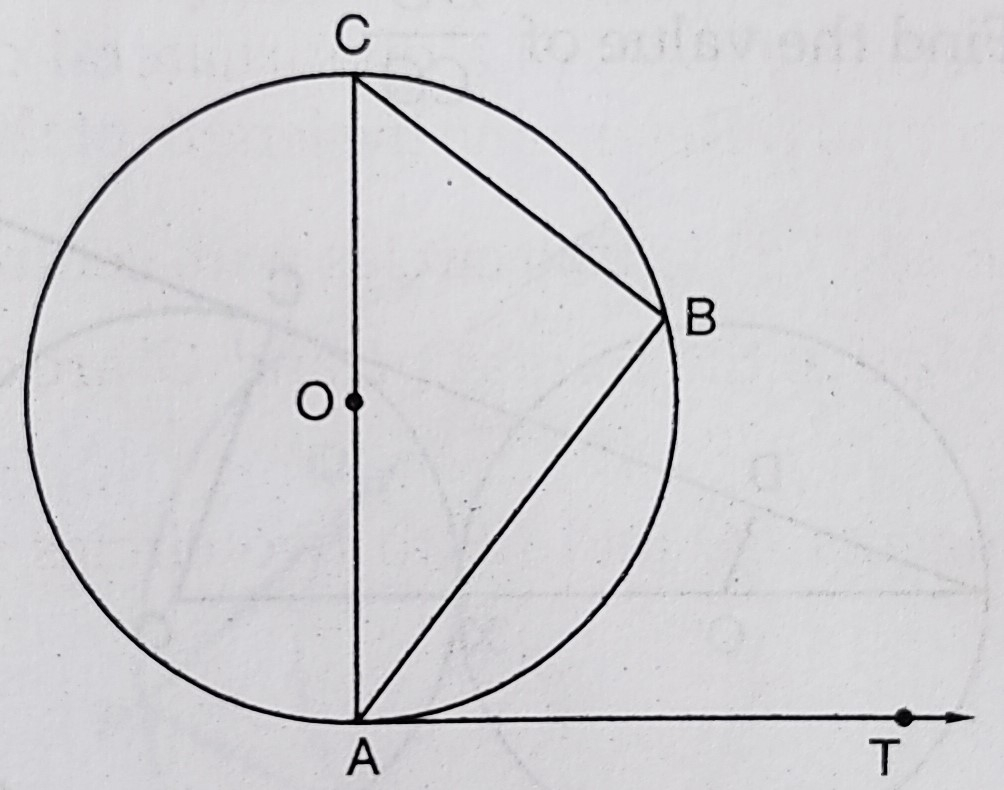

已知

如图所示，$AB$是圆的弦，圆心为$O$，$AOC$是直径，$AT$是$A$点的切线。

需证明：
我们需要证明$∠BAT = ∠ACB$。
 解答

$AC$是直径。

半圆中的角是$90°$。

这意味着：

$∠ABC = 90°$

在$\triangle ABC$中，

$∠CAB + ∠ABC + ∠ACB = 180°$

$∠CAB + ∠ACB = 180° - 90° = 90°$。……….(i)

圆的直径（半径）垂直于切线。

因此，

$CA ⊥ AT$

$∠CAT = 90°$

$∠CAB + ∠BAT = 90°$…….(ii)

由公式(i)和(ii)，

$∠CAB + ∠ACB = ∠CAB + ∠BAT$

$∠ACB = ∠BAT$

证毕。

教程点

更新于：2022年10月10日

48 次浏览

开启您的职业生涯

完成课程获得认证

开始学习