数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装学
法学如图所示，圆的一点 \( C \) 的切线与延长后的直径 \( AB \) 相交于点 \( P \)。如果 \( \angle PCA = 110^{\circ} \)，求 \( \angle CBA \)。
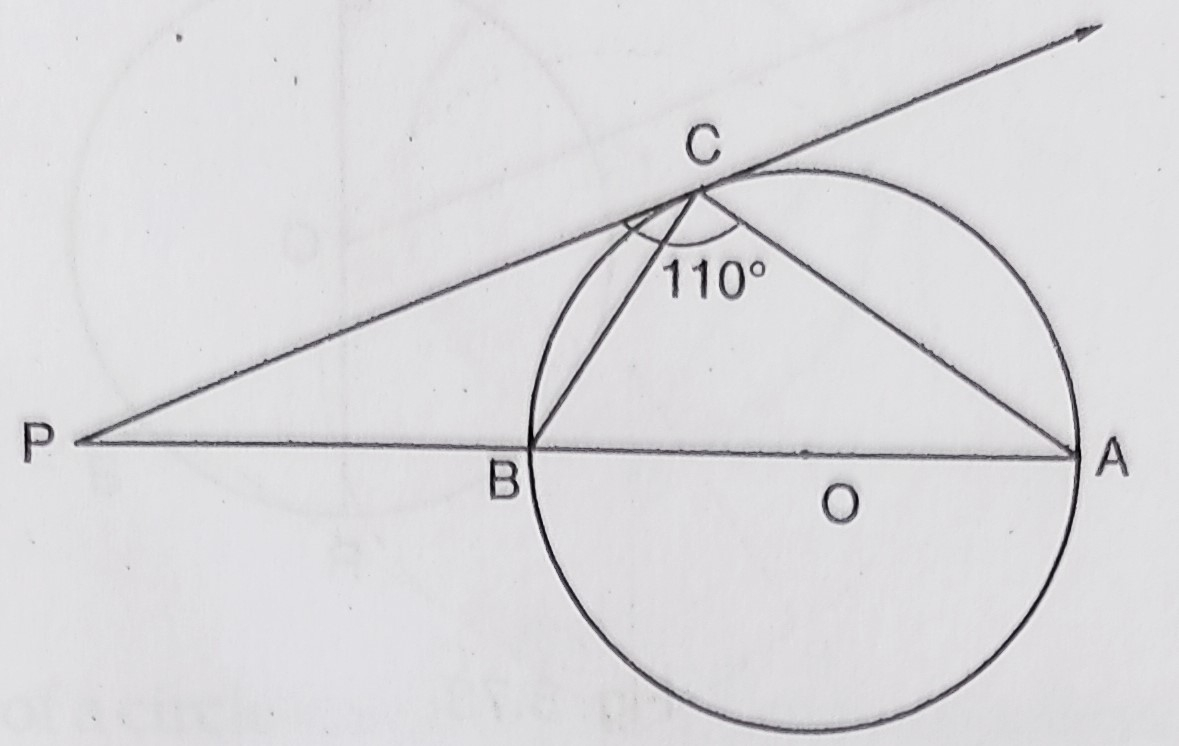
已知
如图所示，圆的一点 \( C \) 的切线与延长后的直径 \( AB \) 相交于点 \( P \)。
\( \angle PCA = 110^{\circ} \).
要求：
求 \( \angle CBA \)
解答
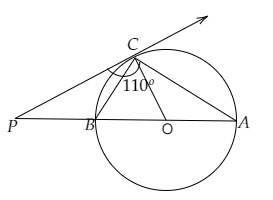
AB是圆的直径，从C点引一条切线，与延长后的直径在P点相交。
连接OC。
圆上任意一点的切线垂直于过该点的半径。
这意味着：
\(OC \perp PC\)
\( \angle PCA = 110^{\circ} \)
\( \angle PCO + \angle OCA = 110^{\circ} \)
\( 90^{\circ} + \angle OCA = 110^{\circ} \)
\( \angle OCA = 110^{\circ} - 90^{\circ} = 20^{\circ} \)
\(OC = OA\) (圆的半径)
\( \angle OCA = \angle OAC = 20^{\circ} \) (等边对等角)
PC是圆的切线。
这意味着：
\( \angle BCP = \angle CAB = 20^{\circ} \) (圆内角与圆外角相等)
在三角形PBC中，
\( \angle P + \angle C + \angle A = 180^{\circ} \)
\( \angle P = 180^{\circ} - (\angle C + \angle A) \)
\( \angle P = 180^{\circ} - (110^{\circ} + 20^{\circ}) \)
\( \angle P = 180^{\circ} - 130^{\circ} = 50^{\circ} \)
在三角形PBC中，
\( \angle BPC + \angle PCB + \angle PBC = 180^{\circ} \)
\( 50^{\circ} + 20^{\circ} + \angle PBC = 180^{\circ} \)
\( \angle PBC = 180^{\circ} - 70^{\circ} \)
\( \angle PBC = 110^{\circ} \)
APB是一条直线。
\( \angle PBC + \angle CBA = 180^{\circ} \)
\( \angle CBA = 180^{\circ} - 110^{\circ} = 70^{\circ} \)
因此，\( \angle CBA = 70^{\circ} \).
浏览量：50
