从外部一点$P$，作圆的切线$P A$和$P B$，圆心为$O$。在圆上一点$E$处作切线，该切线分别与$P A$和$P B$相交于$C$和$D$。如果$P A=14 \mathrm{~cm}$，求$\triangle P C D$的周长。

已知

从外部一点$P$，作圆的切线$P A$和$P B$，圆心为$O$。在圆上一点$E$处作切线，该切线分别与$P A$和$P B$相交于$C$和$D$。

$P A=14 \mathrm{~cm}$。

要求

我们要求出$\triangle P C D$的周长。

解答

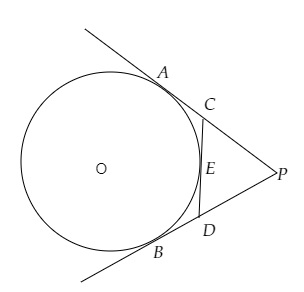
$PA$ 和 $PB$ 是从圆外一点 $P$ 引出的圆的切线，圆心为 $O$。
$CD$ 是圆在点 $E$ 处的另一条切线，它分别与 $PA$ 和 $PB$ 相交于 $C$ 和 $D$。
$PA = 14\ cm$
$PA$ 和 $PB$ 是从 $P$ 引出的圆的切线
$PA = PB = 14\ cm$

$CA$ 和 $CE$ 是从 $C$ 引出的切线

这意味着，

$CA = CE$...….(i)
类似地，

$DB$ 和 $DE$ 是从 $D$ 引出的切线
$DB = DE$....….(ii)
$\triangle PCD$ 的周长 $= PC + PD + CD$

$= PC + PD + CE + DE$

$= PC + CE + PD + DE$

$= PC + CA + PD + DB$     [根据 (i) 和 (ii)]

$= PA + PB$

$= 14 + 14$

$= 28\ cm$

$\triangle PCD$ 的周长是 $28\ cm$。

教程点

更新于: 2022年10月10日

114 次浏览

开启您的职业生涯

通过完成课程获得认证

开始学习