设 \( A \) 为圆外一点，该圆的圆心为 \( O \)，半径为 \( 5 \mathrm{~cm} \)，\( A \) 与 \( O \) 的距离为 \( 13 \mathrm{~cm} \)。\( AP \) 和 \( AQ \) 为圆在 \( P \) 和 \( Q \) 点的切线。若在小弧 \( PQ \) 上一点 \( R \) 作切线 \( BC \)，与 \( AP \) 交于 \( B \) 点，与 \( AQ \) 交于 \( C \) 点，求三角形 \( ABC \) 的周长。

---

已知

\( A \) 为圆外一点，该圆的圆心为 \( O \)，半径为 \( 5 \mathrm{~cm} \)，\( A \) 与 \( O \) 的距离为 \( 13 \mathrm{~cm} \)。\( AP \) 和 \( AQ \) 为圆在 \( P \) 和 \( Q \) 点的切线。

在小弧 \( PQ \) 上一点 \( R \) 作切线 \( BC \)，与 \( AP \) 交于 \( B \) 点，与 \( AQ \) 交于 \( C \) 点。

要求

求三角形 \( ABC \) 的周长。

解题过程

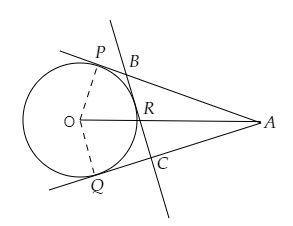
$\angle OPA = 90^o$    (圆上一点的切线垂直于过该点的半径)

在直角三角形 \( OPA \) 中，

$OA^2 = OP^2 + PA^2$    (勾股定理)

$(13)^2 = 5^2 + PA^2$

$PA^2 = 169-25$

$=144$

$=(12)^2$

$\Rightarrow PA = 12\ cm$

三角形 \( ABC \) 的周长 \( = AB + BC + CA \)

$= (AB + BR) + (RC + CA)$

$= AB + BP + CQ + CA$   (因为 \( BR = BP \) 和 \( RC = CQ \)，从圆内一点到圆的两条切线长度相等)

$= AP + AQ$ 

$= 2AP$        (从圆内一点到圆的两条切线长度相等)

$= 2 \times 12$

$= 24\ cm$

三角形 \( ABC \) 的周长为 \( 24\ cm \)。