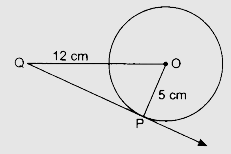
半径为 5 厘米的圆上一点 P 的切线 PQ 与过圆心 O 的一条直线交于点 Q，使得 OQ = 12 厘米。求 PQ 的长度。
(a) 12 厘米
(b) 13 厘米
(c) 8.5 厘米
(d) $\sqrt{199}$ 厘米

已知

半径为 5 厘米的圆上一点 P 的切线 PQ 与过圆心 O 的一条直线交于点 Q，使得 OQ = 12 厘米。

要求

我们需要求 PQ 的长度。

解答：  

圆的半径 = 5 厘米

OQ = 12 厘米

我们知道：

圆的切线垂直于过切点的半径。

∠OPQ = 90°

因此，根据勾股定理，

PQ² + OP² = OQ²

PQ² = OQ² - OP²

PQ² = 12² - 5²

$= 144 - 25$

$= 119$

PQ = $\sqrt{119}$ 厘米

因此，PQ 的长度为 $\sqrt{119}$ 厘米。

教程点

更新于：2022年10月10日

78 次浏览

开启您的 职业生涯

完成课程获得认证

开始学习