求半径为 10 厘米的圆中，一条与圆心距离为 5 厘米的弦的长度。

已知

一条弦与半径为 10 厘米的圆的圆心距离为 5 厘米。

求解

我们需要求弦的长度。

解答


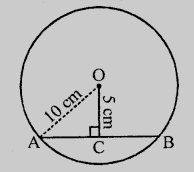
设 AB 为半径为 10 厘米的圆的一条弦。

$OC \perp AB$

这意味着，

$OA = 10\ cm$

$OC = 5\ cm$

$OC$ 将 $AB$ 平分。

$AC = CB$

在直角三角形 $OAC$ 中，

$OA^2 = OC^2 + AC^2$                 (勾股定理)

$(10)^2 = (5)^2 + AC^2$

$100 = 25 + AC^2$

$AC^2 = 100 - 25 = 75$

$\Rightarrow AC = \sqrt{75}$

$= \sqrt{25\times3}$

$= 5 \times 1.732$

$AB = 2 \times AC = 2 \times 5 \times 1.732$

$= 10 \times 1.732$

$= 17.32\ cm$ 

弦的长度为 17.32 厘米。

更新于: 2022年10月10日

341 次查看

开启你的 职业生涯

完成课程并获得认证

开始学习
广告