已知圆的半径为3厘米，弦PQ长4.8厘米。如图所示，P和Q处的切线相交于点T。求TP的长度。

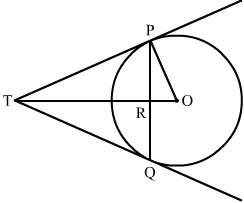
已知：

PQ长度 = 4.8 厘米

圆的半径 = 3 厘米

求解：我们需要求TP的长度。

解：

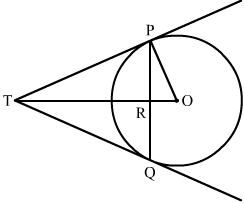
从外一点引出的圆的两条切线的长度相等。所以，

则△TPQ是等腰三角形，TO是∠PTQ的角平分线，在等腰三角形中，角平分线也是高。

因此，∠PRT = ∠PRO = 90^o

所以，

PR = RQ (从圆心到弦的垂线平分弦)

PR = RQ = $\frac{1}{2}$PQ = $\frac{1}{2}$ × 4.8 = 2.4 厘米

在Rt△PRO中，由勾股定理

OR² = OP² - PR²

OR² = 3² - 2.4²

OR² = 9 - 5.76

OR = $\sqrt{3.24}$

OR = 1.8 厘米

在Rt△TPR中，∠PRT = 90^o

则

∠TPR + ∠PTR = 90^o …..(1)

又

∠TPO = 90^o (圆的切线垂直于过切点的半径)

∠TPR + ∠RPO = 90^o …..(2)

由(1)和(2):

∠TPR + ∠PTR = ∠TPR + ∠RPO

∠PTR = ∠RPO …..(3)

教程点

更新于：2022年10月10日

浏览量：607

启动您的职业生涯

完成课程获得认证

开始学习