如图，$P O \perp Q 0$。在$P$和$Q$处的圆的切线相交于一点$T$。证明$P Q$和$O T$是彼此的垂直平分线。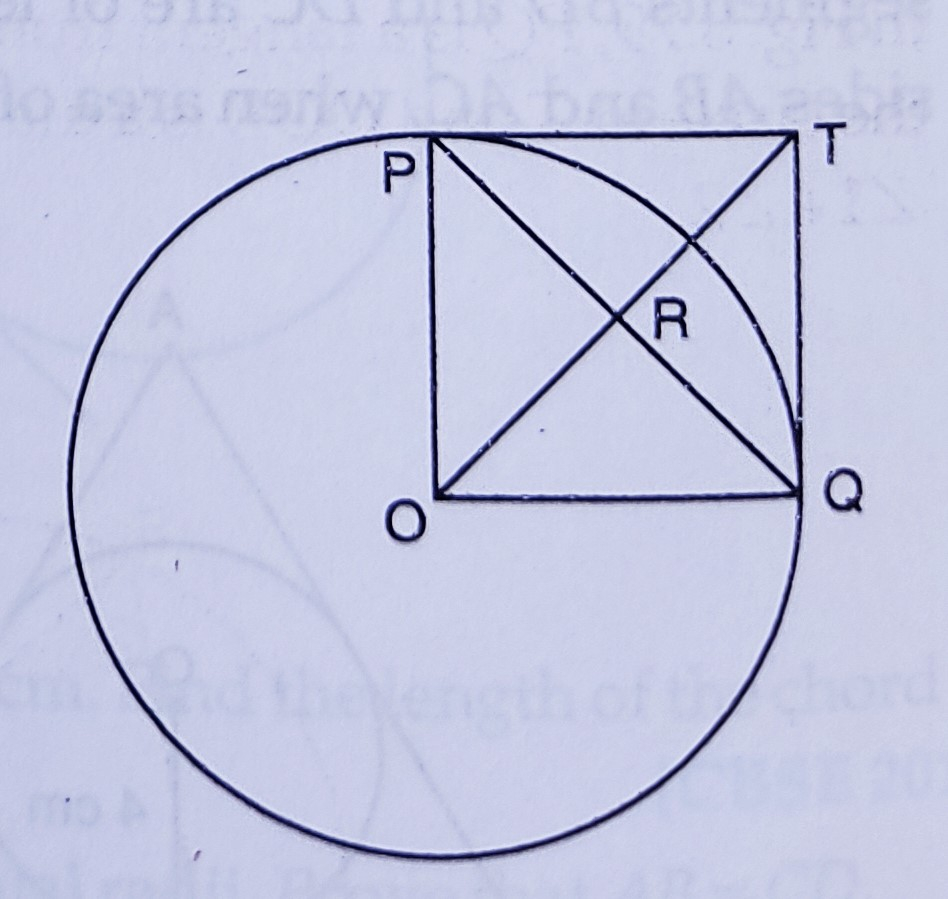"\n

已知

如图，$P O \perp Q 0$。在$P$和$Q$处的圆的切线相交于一点$T$。

需要证明：
我们需要证明$P Q$和$O T$是彼此的垂直平分线。

 解答

$PT$ 和 $QT$ 是圆的切线。

$PT = QT$

$PO\ \perp\ QO$

$OP$ 和 $OQ$ 是圆的半径，并且 $\angle POQ = 90^o$

$OQTP$ 是一个正方形，其中 $PQ$ 和 $OT$ 是对角线。

正方形的对角线互相垂直平分。

$PQ$ 和 $OT$ 互相垂直平分。

因此，$PQ$ 和 $QT$ 是彼此的垂直平分线。

证毕。

教程点

更新于： 2022年10月10日

69 次浏览

开启您的 职业生涯

完成课程获得认证

开始学习