两个圆在点$P$处外切。从$P$处切线上的一个点$T$，分别作圆的切线$T O$和TR，切点分别为$Q$和$R$。证明$TQ = TR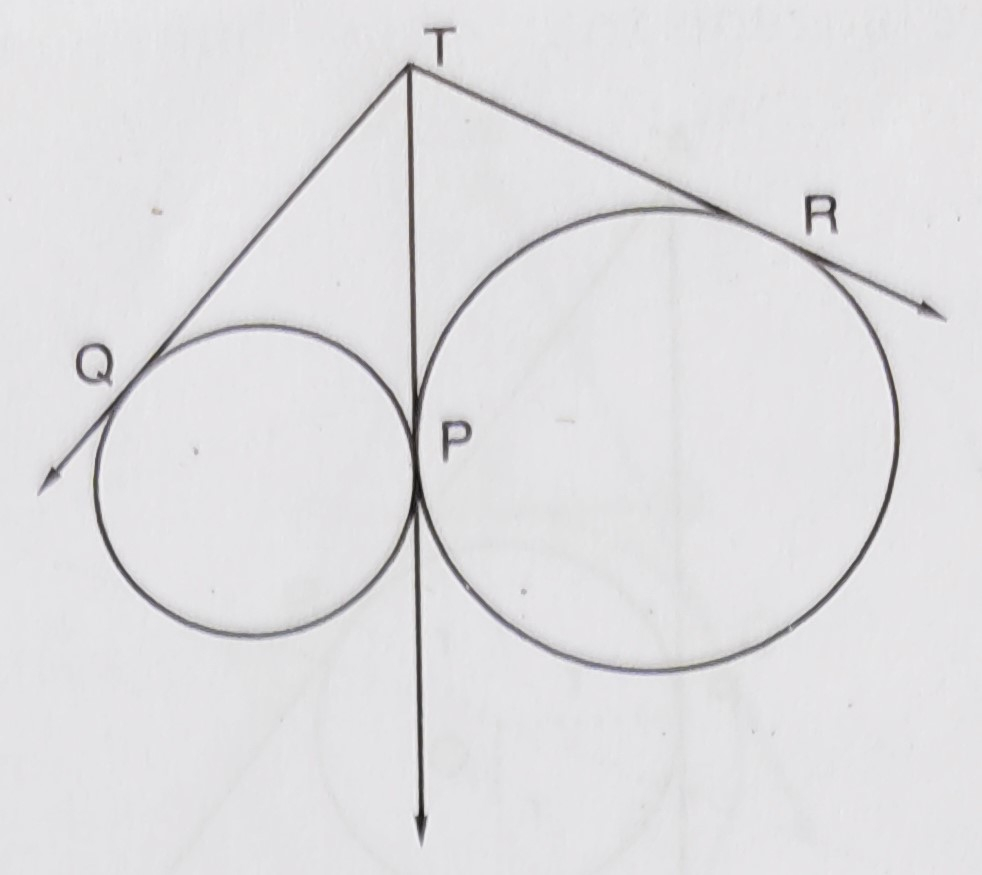$。"\n

已知

两个圆在点$P$处外切。从$P$处切线上的一个点$T$，分别作圆的切线$T O$和TR，切点分别为$Q$和$R$。

要求

我们需要证明$TQ = TR$。

解答

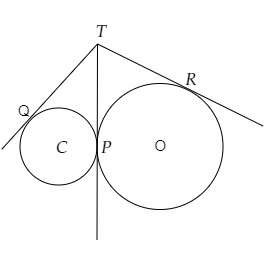
从点$T$，$TR$和$TP$是到以$O$为圆心的圆的两条切线。

这意味着，

$TR = TP$....….(i)

同样地，

从点$T$，$TQ$和$TP$是到以$C$为圆心的圆的两条切线。

$TQ = TP$...….(ii)

从(i)和(ii)，我们得到，

$TQ = TR$

证毕。

教程点

更新于: 2022年10月10日

48 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习