如果从两条相交圆的公共弦上的任意一点作切线，证明这两条切线相等。

已知

从两条相交圆的公共弦上的任意一点作切线。

要求

我们必须证明它们相等。

解答


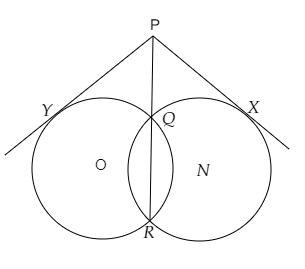
设QR为两圆的公共弦，两圆在Q和R点相交。

P为QR延长线上的点。

PY和PX分别为分别以O和C为圆心的圆的切线。

证明

PY是切线，PQR是过P点的割线，圆心为O。

这意味着：

PY² = PQ × PR……(i)

类似地：

PX是切线，PQR是过P点的割线，圆心为C。

这意味着：

PX² = PQ × PR……(ii)

由(i)和(ii)可得：

PY² = PX²

PY = PX

证毕。

更新于：2022年10月10日

553 次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告