以三角形的边为直径作圆。证明任意两边的圆在第三边（或第三边的延长线）上相交。

已知

以三角形的边为直径作圆。

要证明

我们必须证明任意两边的圆在第三边（或第三边的延长线）上相交。

解答

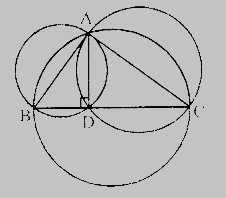
在△ABC中，以AB和AC为直径作圆。

作AD⊥BC


AD⊥BC

这意味着：

∠ADB = ∠ADC = 90°

从图中可以看出：

以AB和AC为直径所作的圆将经过D点。

因此，以三角形的两边为直径所作的圆经过位于第三边的D点。

更新于：2022年10月10日

76 次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告