利用射影定理的逆定理，证明连接三角形任意两边中点的直线平行于第三边。

待办事项

利用射影定理的逆定理，我们需要证明连接三角形任意两边中点的直线平行于第三边。

解答

在△ABC中，设D为AB的中点。

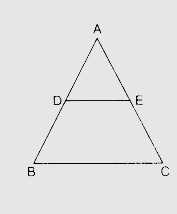
在△ABC中，

这意味着，

$\frac{AD}{DB}=1$.........(i)

$\frac{AE}{EC}=1$........(ii)

因此，

$\frac{AD}{DB}=\frac{AE}{EC}$

这意味着，根据射影定理的逆定理，

$DE \| BC$

证毕。

教程点

更新于：2022年10月10日

34 次查看

开启你的职业生涯

完成课程获得认证

开始学习