证明圆弧中点处的切线平行于连接该弧端点的弦。

已知：圆弧中点处的一条切线平行于连接该弧端点的弦。

目标：证明圆弧中点处的切线平行于连接该弧端点的弦。

解答
在图中，C 是劣弧 PQ 的中点，O 是圆心，AB 是过点 C 的圆的切线。

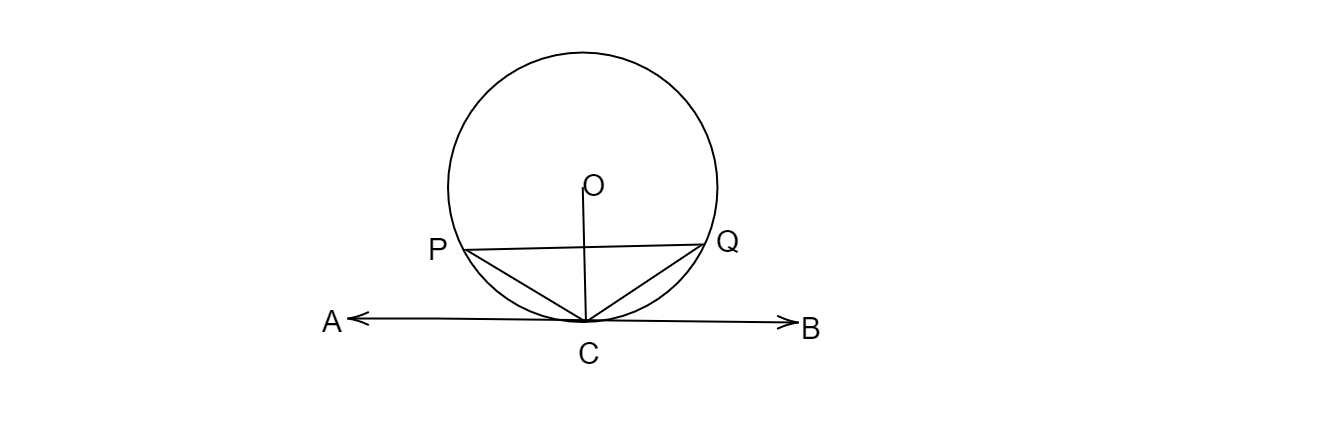
我们必须证明，在圆的弧 PQ 的中点处画出的切线平行于连接弧 PQ 端点的弦。

我们将证明 PQ ∥ AB。

已知 C 是弧 PQ 的中点。

因此，弧 PC = 弧 CQ。

PC = CQ

这表明

△PQC 是等腰三角形。

因此，△PQC 的边 PQ 的垂直平分线经过顶点 C。

弦的垂直平分线经过圆心。

因此，PQ 的垂直平分线经过圆心 O。

因此，PQ 的垂直平分线经过点 O 和 C。

因此，PQ ⊥ OC

AB 是过圆上点 C 的圆的切线。

因此，AB ⊥ OC

弦 PQ 和圆的切线 PQ 与同一条直线 OC 垂直。

PQ ∥ AB。
 

更新于：2022 年 10 月 10 日

130 次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告