证明从圆外一点引出的两条切线之间的夹角与连接切点并在圆心处所成的角互补。

待办事项

我们需要证明从圆外一点引出的两条切线之间的夹角与连接切点并在圆心处所成的角互补。

解答

设 $PA$ 和 $PB$ 是两条切线，$A$ 和 $B$ 是切点的坐标。

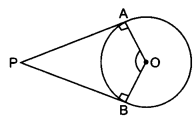
$\mathrm{OA} \perp \mathrm{AP}$

$\mathrm{OB} \perp \mathrm{BP}$

$\angle \mathrm{OAP}=\angle \mathrm{OBP}=90^{\circ}$

在四边形 $\mathrm{OAPB}$ 中

$\angle \mathrm{OAP}+\angle \mathrm{OBP}+\angle \mathrm{APB}+\angle \mathrm{AOB}=360^{\circ}$

$90^{\circ}+90^{\circ}+\angle \mathrm{APB}+\angle \mathrm{AOB}=360^{\circ}$

$\angle \mathrm{APB}+\angle \mathrm{AOB}=360^{\circ}-180^{\circ}$

$=180^{\circ}$

因此，

$\angle \mathrm{APB}$ 和 $\angle \mathrm{AOB}$ 是互补角。

证毕。

教程点

更新于: 2022年10月10日

113 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习