数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学证明两条平行切线之间的切线截距在圆心处构成直角。
待办事项
我们必须证明两条平行切线之间的切线截距在圆心处构成直角。
解答
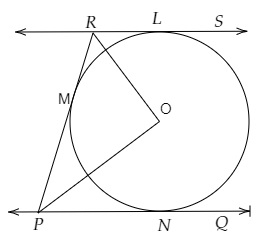
设PQ和RS是圆的两条平行切线。
RMP是PQ和RS之间切线的截距。
连接RO和PQ，其中O是圆心。
RL和RM是切线，连接RO。
这意味着：
∠LRO = ∠MRO .......(i)
同样地：
PM和PN是切线，连接PO。
∠NPO = ∠MPO .......(ii)
将方程式(i)和(ii)相加，我们得到：
∠LRO + ∠NPO = ∠MRO + ∠MPO
∠LRM + ∠MPN = 180° (同旁内角)
⇒ ∠LRO + ∠MRO + ∠MPO + ∠NPO = 180°
⇒ ∠MRO + ∠MRO + ∠MPO + ∠MPO = 180°
⇒ 2(∠MRO + ∠MPO) = 180°
⇒ ∠MRO + ∠MPO = 180°/2 = 90°
在△POR中：
∠MRO + ∠MPO + ∠POR = 180°
⇒ 90° + ∠POR = 180°
⇒ ∠POR = 180° - 90°
∠POR = 90°
证毕。
更新于：2022年10月10日
85 次浏览
广告