数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法学在给定的图形中，XY 和 X'Y' 是与圆心 O 相切的两条平行切线，另一条切线 AB 与圆在 C 点相切，并分别与 XY 相交于 A 点和 X'Y' 相交于 B 点。证明∠AOB = 90°。
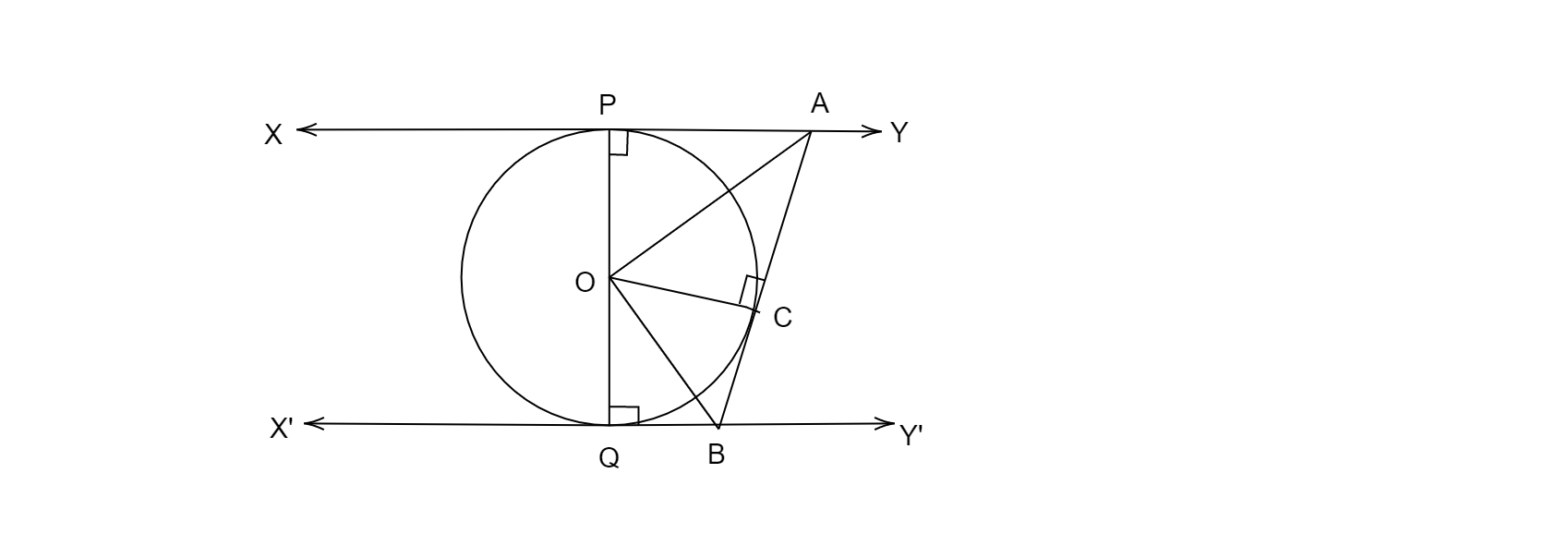
已知：圆心为 O 的圆，两条平行切线 XY 和 X'Y' 与圆相切，另一条切线在 C 点与圆相切，分别与 XY 和 X'Y' 交于 A 和 B。
求证：∠AOB = 90°
解
XY 和 X'Y' 是圆心为 O 的圆的两条平行切线，分别与圆相切于 P 和 Q。
AB 是在 C 点与圆相切的切线，它分别与 XY 交于 A 点，与 X'Y' 交于 B 点。
步骤如下
连接 OC。
在△OAP 和△OAC 中，
OP = OC (同圆半径)
AP = AC (从外一点到圆的两条切线长相等)
OA = OA (公共边)
△OAP ≅ △OAC (SSS 全等)
∠AOP = ∠AOC …(1)
类似地，△OBC ≅ △OBQ
∠BOQ = ∠BOC …(2)
现在，AOB 是圆的直径，因此是一条直线。
∠AOP + ∠AOC + ∠BOQ + ∠BOC = 180°
由 (1) 和 (2)，
我们有：2∠AOC + 2∠BOC = 180°
∠AOC + ∠BOC = 180°/2
= 90°
我们知道 ∠AOC + ∠BOC = ∠AOB = 90°
=> ∠AOB = 90°
因此，∠AOB = 90° 得证。
更新于：2022年10月10日
浏览量：103
广告