如图所示，$O$是圆心，$BCD$在$C$点与圆相切。证明$\angle BAC+\angle ACD=90^{\circ}$。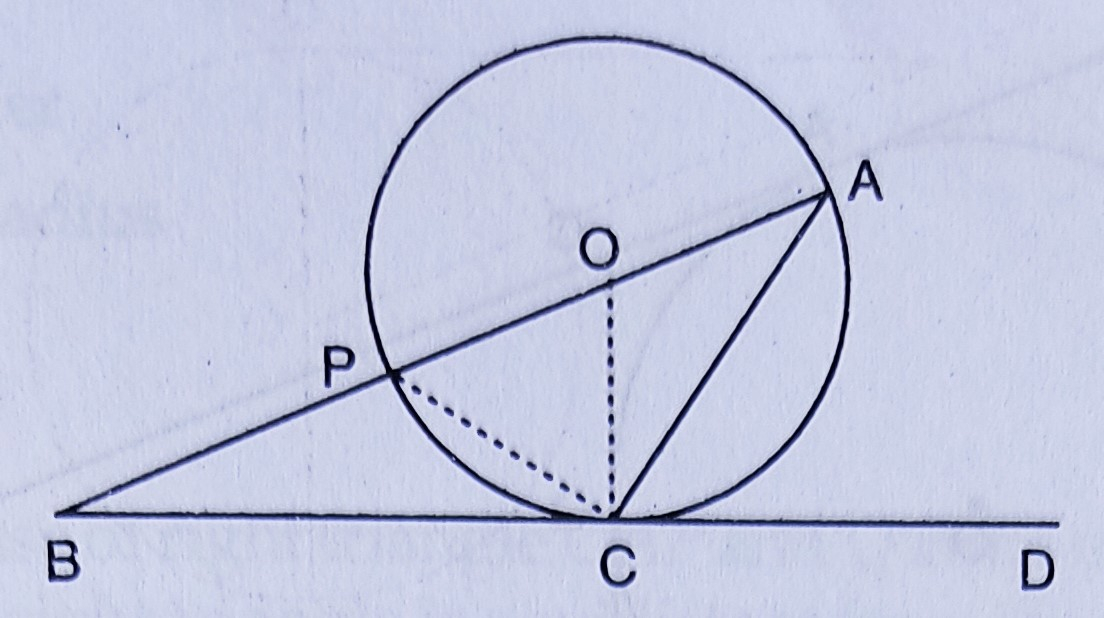

已知

如图所示，$O$是圆心，$BCD$在$C$点与圆相切。

需要证明：
我们需要证明$\angle BAC+\angle ACD=90^{\circ}$.

 解答

由图可知：

$\angle ACD = \angle CPA$ (圆内角与弦所对的圆周角相等)

在$\triangle ACP$中，

$\angle ACP = 90^o$ (半圆上的圆周角)

$\angle PAC + \angle CPA = 90^o$

$\angle BAC + \angle ACD = 90^o$ ($\angle ACD = \angle CPA$)

证毕。

Tutorialspoint

更新于：2022年10月10日

45 次浏览

开启您的职业生涯

完成课程获得认证

开始学习