在给定的图形中，$OC$ 和 $OD$ 分别是$∠BCD$ 和 $∠ADC$ 的角平分线。如果$∠A = 105°$，求$∠B$。

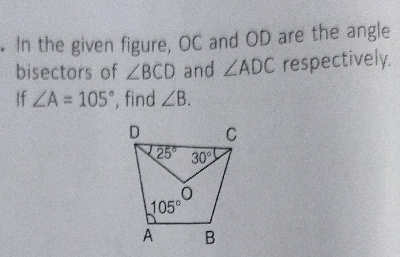
已知：在给定图形中，$OC$ 和 $OD$ 分别是 $\angle BCD$ 和 $\angle ADC$ 的角平分线，且 $\angle A = 105°$。

求解：求 $\angle B$。

解

$\because OD$ 是 $ADC$ 的平分线

$\therefore OC$ 是 $BCD$ 的平分线

$\Rightarrow \angle ADC = \angle D = 2\times\angle ODC$

$\Rightarrow \angle D = 25° \times 2 = 50°$

类似地：$\angle BCD = \angle C = 2\times\angle OCD$

$\Rightarrow \angle C = 30° \times 2 = 60°$

已知 $A + B + C + D = 360°$ (四边形的内角和为 $360°$)

$\Rightarrow 105° + B + 60° + 50° = 360°$

$\Rightarrow 105° + B + 110° = 360°$

$\Rightarrow B + 105° + 110° = 360°$

$\Rightarrow B + 215° = 360°$

$\Rightarrow B = 360° - 215°$

$\Rightarrow B = 145°$

因此，$\angle B = 145°$。

Tutorialspoint

更新于：2022年10月10日

387 次浏览

开启你的职业生涯

完成课程获得认证

开始学习