证明与圆的切线在切点处的垂线经过圆心。

待办事项

我们需要证明与圆的切线在切点处的垂线经过圆心。

解答

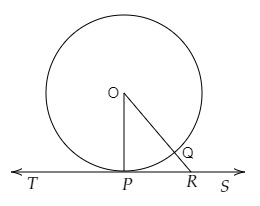
设 $TS$ 是以 $O$ 为圆心，在 $P$ 点与圆相切的切线。

连接 $OP$。

画一条直线 $OR$，该直线与圆相交于 $Q$ 点，并与切线 $TS$ 相交于 $R$ 点。

$OP = OQ$ (圆的半径)

$OQ

$\Rightarrow OP

同样地，

$OP$ 小于从 $O$ 到 $TS$ 的所有其他直线。

$OP$ 是最短的直线。

因此，

$OP$ 垂直于 $TS$。

通过 $P$ 的垂线将经过圆心。

证毕。 

教程点

更新于： 2022年10月10日

54 次浏览

开启你的 职业生涯

通过完成课程获得认证

立即开始