证明以菱形任意一边为直径的圆，经过其对角线的交点。

待办事项

我们需要证明以菱形任意一边为直径的圆，经过其对角线的交点。

解答

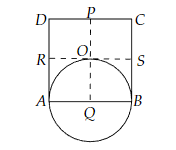
以 Q 为圆心画一个圆。

该圆经过 A、B 和 O，如图所示。

这意味着：

$QA = QB = QO$      (圆的半径)

我们知道：

菱形的各边相等。

这意味着：

$AB = CD$

两边同时乘以 $\frac{1}{2}$，得到：

$\frac{1}{2}AB = \frac{1}{2}CD$

$\Rightarrow AQ = DP$

$BQ = DP$

$Q$ 是 $AB$ 的中点

这意味着：

$AQ= BQ$.........(i)

同样地：

$RA = SB$

画一条平行于 $AD$ 的线段 $PQ$

$RA = QO$.........(ii)

由 (i) 和 (ii) 可得：

$QA = QB = QO$

证毕。

教程点

更新于: 2022年10月10日

57 次浏览

开启你的 职业生涯

通过完成课程获得认证

立即开始