证明圆的直径两端所作的切线平行。

待办事项

我们需要证明圆的直径两端所作的切线平行。

解答

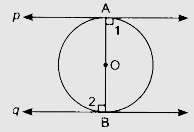
设 $AB$ 为圆的直径，$p$ 和 $q$ 为两条切线。

$OA \perp p$

$OB \perp q$

$\angle 1 = \angle 2 = 90^o$

这意味着，

$p \| q$          (垂直于同一条直线的两条直线互相平行)

证毕。

教程点

更新于: 2022年10月10日

343 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习