证明：平分圆内弦的直径也平分该弦在圆心处所张的角。

待办事项

我们需要证明：平分圆内弦的直径也平分该弦在圆心处所张的角。

解答

设在圆心为O的圆中，CD为直径，AB为弦

且直径在E点平分弦AB。

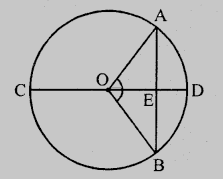
连接OA和OB。

在△OAE和△OBE中，

OA = OB             (圆的半径)

OE = OE           (公共边)

AE = EB          (已知)

因此，根据SSS公理，

△OAE ≅ △OBE

这意味着，

∠AOE = ∠BOE         (全等三角形对应角相等)

因此，直径平分弦所张的角。

证毕。

教程点

更新于：2022年10月10日

253 次浏览

开启你的职业生涯

完成课程获得认证

开始学习