证明外切于圆的四边形的对边在圆心处所张的角互为补角。

待办事项

我们需要证明外切于圆的四边形的对边在圆心处所张的角互为补角。

解答

设四边形 $ABCD$ 是外切于圆心为 $O$ 的圆的四边形。

$AB$ 在点 $P$ 处与圆相切。

类似地，

$BC、CD$ 和 $DA$ 分别在 $Q、R$ 和 $S$ 处与圆相切。

连接 $OA、OB、OC、OD$ 和 $OP、OQ、OR、OS$。

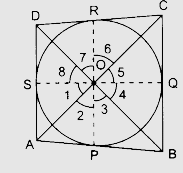
$OA$ 平分 $\angle \mathrm{POS}$

$\angle 1=\angle 2$

$\angle 3=\angle 4$

$\angle 5=\angle 6$

$\angle 7=\angle 8$

因此，

$\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7+\angle 8=360^{\circ}$

$\angle 1+\angle 1+\angle 4+\angle 4+\angle 5+\angle 5+\angle 8+\angle 8=360^{\circ}$

$2[\angle 1+\angle 4+\angle 5+\angle 8]=360^{\circ}$

$(\angle 1+\angle 8+\angle 4+\angle 5)=180^{\circ}$

$\angle \mathrm{AOD}+\angle \mathrm{BOC}=180^{\circ}$

类似地，

$\angle \mathrm{AOB}+\angle \mathrm{COD}=180^{\circ}$

因此，外切于圆的四边形的对边在圆心处所张的角互为补角。

教程点

更新于: 2022年10月10日

85 次浏览

开启您的 职业生涯

通过完成课程获得认证

开始学习