如果四边形的边都与一个圆相切，证明一对对边的和等于另一对对边的和。

已知

四边形的边与一个圆相切。

任务

我们必须证明一对对边的和等于另一对对边的和。

解答


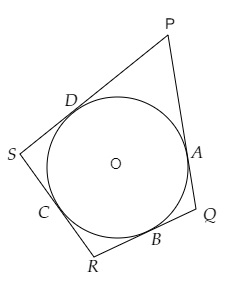
设四边形PQRS的边分别与圆在A、B、C和D处相切。

证明

PA和PD是从P点到圆的切线。

这意味着：

PA = PD……(i)

类似地：

QA = QB……(ii)

RC = RB……(iii)

SC = SD……(iv)

将方程(i)、(ii)、(iii)和(iv)相加，我们得到：

PA + QA + SC + RC = RB + QB + SD + PD

PQ + RS = RQ + PS

证毕。

更新于：2022年10月10日

浏览量：57

启动您的职业生涯

完成课程获得认证

开始学习
广告