证明平行四边形的对角线平方和等于其边长平方和。

待办事项

我们需要证明平行四边形的对角线平方和等于其边长平方和。

解答

我们知道：

平行四边形的对角线互相平分。

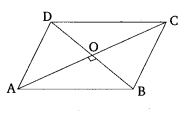
设平行四边形为ABCD，对角线AC和BD相交于点O。

这意味着：

BO和DO分别是三角形ABC和ADC的中线。

$\mathrm{AB}^{2}+\mathrm{BC}^{2}=2 \mathrm{BO}^{2}+\frac{1}{2} \mathrm{AC}^{2}$...........(i)

$\mathrm{AD}^{2}+\mathrm{CD}^{2}=2 \mathrm{OD}^{2}+\frac{1}{2} \mathrm{AC}^{2}$...........(ii)

(i)和(ii)相加，得到：

$\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CD}^{2}+\mathrm{AD}^{2}=2(\mathrm{BO}^{2}+\mathrm{OD}^{2})+\mathrm{AC}^{2}$

$=2(\frac{1}{4} \mathrm{BD}^{2}+\frac{1}{4} \mathrm{BD}^{2})+\mathrm{AC}^{2}$      (因为 $\mathrm{DO}=\mathrm{BO}=\frac{1}{2} \mathrm{BD}$)

$=2 \times \frac{1}{2} \mathrm{BD}^{2}+\mathrm{AC}^{2}$

$\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CD}^{2}+\mathrm{AD}^{2}=\mathrm{AC}^{2}+\mathrm{BD}^{2}$

证毕。

教程点

更新于：2022年10月10日

90 次浏览

开启你的职业生涯

完成课程获得认证

开始学习